다각형 순열 완벽 정복 (직사각형/정삼각형 탁자 경우의 수 풀이)
실제 세상의 탁자가 모두 완벽한 원 모양은 아니겠죠? 직사각형, 정사각형, 정삼각형처럼 다양한 모양의 탁자에 둘러앉는 경우의 수는 어떻게 계산해야 할까요? 이를 ‘다각형 순열’ 또는 ‘탁자 순열’이라고 부릅니다.
많은 교재에서 `(원순열의 수) × (회전 시 겹치지 않는 자리의 수)` 라는 공식을 제시하지만, 왜 이런 공식이 나왔는지 이해하지 못하면 조금만 다른 모양이 나와도 금방 혼란에 빠지게 됩니다. 오늘은 이 공식의 의미를 근본적인 원리부터 파헤치고, 어떤 모양의 탁자가 나와도 자신 있게 풀 수 있는 두 가지 핵심 전략을 상세한 설명과 함께 알려드리겠습니다.
이 글 하나로 다각형 순열에 대한 모든 두려움을 없애드리겠습니다!
🎯 다각형 순열의 본질: ‘서로 다른 자리’는 몇 개인가?
다각형 순열은 순수한 원순열과 직선 순열의 특징을 모두 가진 ‘하이브리드’ 개념입니다. 원탁처럼 회전하면 같아지는 경우가 있지만, 직선 배열처럼 모든 자리가 동등하지는 않기 때문입니다.
핵심은 이것입니다: “첫 번째 사람이 어느 자리에 앉느냐에 따라 완전히 다른 경우가 생길 수 있다.”
예를 들어, 문제에 제시된 직사각형 탁자를 봅시다. 이 탁자에는 6개의 자리가 있습니다. 과연 이 6개의 자리는 모두 같은 가치를 가질까요? 그렇지 않습니다. 내가 어느 자리에 앉느냐에 따라 보이는 풍경(상대적인 위치 관계)이 달라집니다.
⭐ 회전시켰을 때 겹치지 않는 ‘서로 다른 자리’ 찾기
6개의 자리에 1번부터 6번까지 번호를 매겨봅시다.
6개의 자리에 1번부터 6번까지 번호를 매겨봅시다.
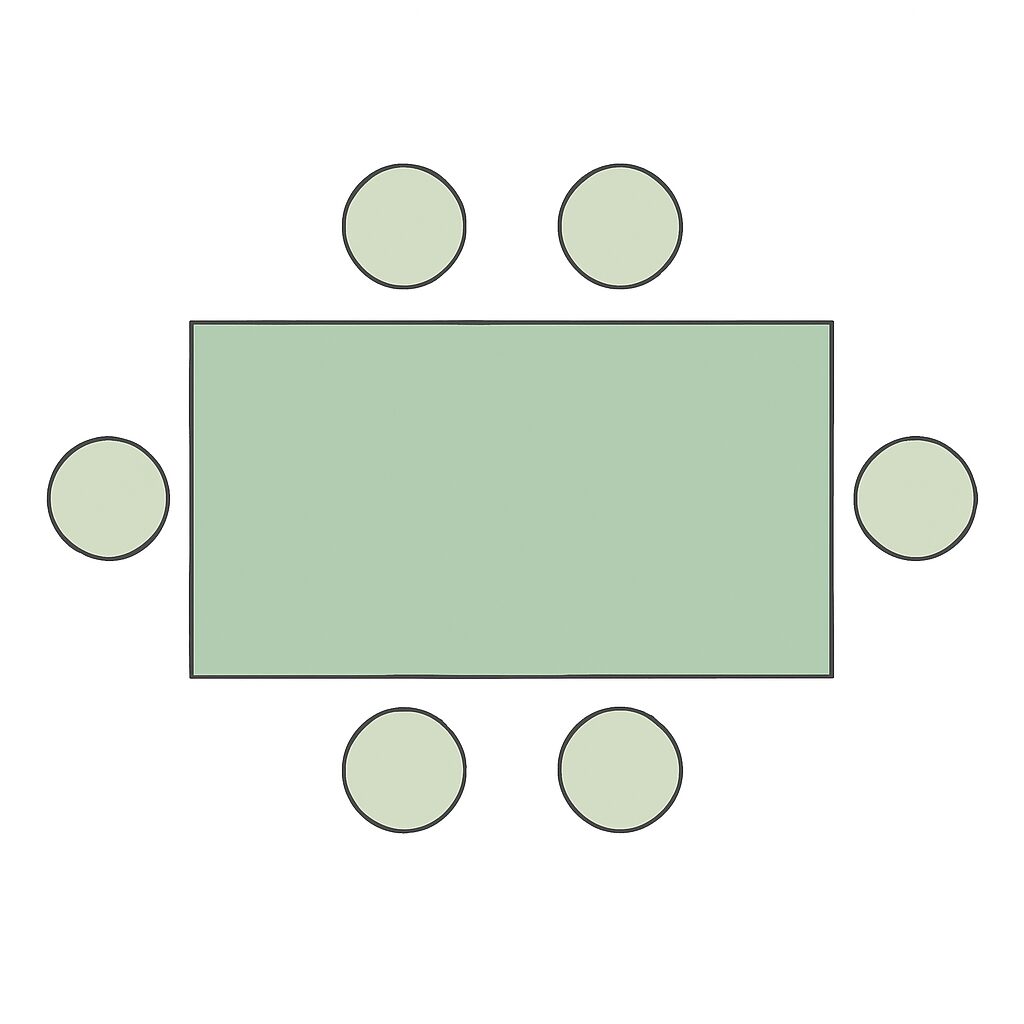
- 1번 자리에 앉았다고 상상해 보세요. 짧은 변의 가운데 자리입니다.
- 2번 자리에 앉아보세요. 긴 변의 모서리 쪽 자리입니다.
- 3번 자리에 앉아보세요. 긴 변의 다른 모서리 쪽 자리입니다.
이제 탁자를 180도 회전시켜 봅시다.
- 4번 자리는 1번 자리와 겹쳐집니다. (본질적으로 같은 종류의 자리)
- 5번 자리는 2번 자리와 겹쳐집니다. (같은 종류의 자리)
- 6번 자리는 3번 자리와 겹쳐집니다. (같은 종류의 자리)
결론적으로, 이 직사각형 탁자에는 회전을 고려했을 때 서로 다른 종류의 자리가 3가지 (1번, 2번, 3번) 있다는 것을 알 수 있습니다. 이것이 바로 다각형 순열 문제 해결의 첫 단추입니다.
✏️ 실력 다지기: 직사각형 탁자 문제 풀이
문제: 오른쪽 그림과 같은 직사각형 모양의 탁자에 6명이 둘러앉는 경우의 수는? (단, 회전하여 일치하는 것은 같은 것으로 본다.)
🔍 방법 1: 교재 공식 활용법 (원순열 × 다른 자리 수)
가장 빠르고 직관적인 풀이법입니다. 위에서 찾은 ‘서로 다른 자리의 수’를 원순열 공식에 곱해주는 방식입니다.
Step 1: 기본적인 원순열의 수 계산하기
만약 이 탁자가 완벽한 원형이었다고 가정하고, 6명을 앉히는 원순열의 수를 계산합니다.
$$ (6-1)! = 5! = 120 \text{가지} $$
Step 2: 서로 다른 자리의 수 파악하기
위의 개념 설명에서 확인했듯이, 이 직사각형 탁자에는 회전했을 때 겹쳐지지 않는 서로 다른 종류의 자리가 총 3가지 있습니다.
Step 3: 두 결과 곱하기
원순열의 수에 서로 다른 자리의 수를 곱하여 최종 답을 구합니다.
$$ (\text{원순열의 수}) \times (\text{다른 자리의 수}) = 120 \times 3 = 360 \text{가지} $$
이 방법은 매우 빠르지만, ‘다른 자리의 수’를 정확하게 세는 것이 관건입니다.
💡 방법 2: 근본 원리 활용법 (전체 직선 순열 ÷ 대칭성)
이 방법은 공식의 원리를 파고드는, 더 근본적인 풀이법입니다. 모든 다각형 순열에 적용할 수 있는 만능 열쇠와 같습니다.
Step 1: 모든 자리가 다르다고 가정하고 직선 순열 계산하기
우선 회전은 없다고 생각하고, 6개의 서로 다른 자리에 6명을 배열하는 경우의 수를 구합니다. 즉, 일반적인 순열입니다.
$$ 6! = 720 \text{가지} $$
Step 2: 회전 대칭성 파악하기 (중복되는 경우의 수)
이제 이 탁자를 회전시켰을 때 몇 번이나 자기 자신과 똑같이 겹쳐지는지(대칭성)를 찾습니다. 이 횟수가 바로 중복되는 경우의 수가 됩니다.
- 0도 회전: 원래 모습 (당연히 겹쳐짐)
- 180도 회전: 완전히 겹쳐짐
- 360도 회전은 0도 회전과 같습니다.
따라서 이 직사각형 탁자는 회전시켰을 때 총 2번 겹쳐집니다. 즉, 하나의 배열이 2번씩 중복되어 계산된 것입니다.
Step 3: 전체 경우를 대칭성으로 나누기
Step 1에서 구한 전체 직선 순열의 수를 Step 2에서 구한 회전 대칭성(중복 횟수)으로 나누어 줍니다.
$$ \frac{\text{전체 순열의 수}}{\text{회전 대칭성}} = \frac{6!}{2} = \frac{720}{2} = 360 \text{가지} $$
역시 정확히 같은 결과가 나옵니다! 이 방법은 ‘다른 자리’를 세는 실수를 줄여주고, 더 복잡한 도형에도 일관되게 적용할 수 있는 장점이 있습니다.
최종 정답: 6명이 직사각형 탁자에 둘러앉는 경우의 수는 ③ 360가지 입니다.
✨ 최종 정리 및 마무리
오늘은 원순열의 응용 버전인 다각형 탁자 순열에 대해 알아보았습니다. 핵심은 더 이상 모든 자리가 동등하지 않다는 것을 인지하는 것입니다.
- 빠른 풀이 (교재 공식):
(n-1)! × (다른 자리의 수). ‘다른 자리’의 개수만 정확히 셀 수 있다면 가장 효율적입니다. - 근본 풀이 (대칭성 활용):
n! ÷ (회전 대칭성). 도형의 회전 대칭성을 파악하여 전체 순열에서 중복을 제거하는 원리적인 방법으로, 더 안정적이고 모든 도형에 적용 가능합니다.
예를 들어, 정삼각형 탁자(각 변에 2명씩, 총 6명)라면 ‘다른 자리’는 2개(모서리, 가운데), 회전 대칭성은 3번이므로, $ (6-1)! \times 2 = 240 $ 또는 $ 6! \div 3 = 240 $ 으로 동일한 결과를 얻을 수 있습니다. 두 가지 방법을 모두 익혀두고, 문제 상황에 맞게 더 편리한 전략을 선택하는 지혜를 기르시길 바랍니다. 오늘도 수고 많으셨습니다!
원순열 기초 개념 정리 – 확률과 통계 (단순 암기는 이제 그만! 원리부터 이해하기)